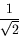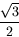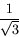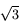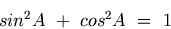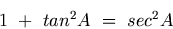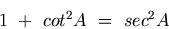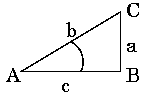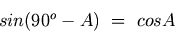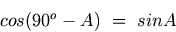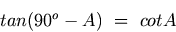Matemática : Trigonometria
Valores de Funções Trigonométricas para Ângulos ComunsÉ de grande utilidade saber os valores das funções trigonométricas para certos ângulos comuns. Os valores das funções trigonométricas para ângulos de 0, 30o, 45o, 60o e 90o são dados na tabela abaixo.
É possível obter os valores na tabela acima para 0, 45o e 90o usando-se as definições do Módulo de Trigonometria 1.
Os valores na tabela acima podem ser facilmente lembrados usando-se o seguinte macete para memorização.
Os valores de sen 0, sen 30o, sen 45o, sen 60o e sen 90o são simplesmente dados pelas raízes quadradas de 0/4, 1/4, 2/4, 3/4 e 4/4.
Os valores de cos 0, cos 30o, cos 45o, cos 60o e cos 90o são dados pelas raízes quadradas de 4/4, 3/4, 2/4, 1/4 e 0/4. Obviamente, os valores da tan para qualquer ângulo são obtidos ao se dividir o valor do seno pelo valor do coseno.
Identidades Trigonométrica ImportantesAlgumas importantes identidades trigonométricas relacionando funções de um ângulo (digamos, A) são dadas abaixo.
Estas identidades são úteis na simplificação e solução de problemas. Suas provas são dadas abaixo.
Propriedade CofunçãoA propriedade cofunção é muito importante e é dada abaixo.
A propriedade cofunção é fácil de se provar ao se começar com o fato de que a soma dos três ângulos de um triângulo é sempre 180o, ou seja, A + B + C = 180o. Para um triângulo retângulo, o ângulo B é 90o e A + C = 90o. Ao se usar 90o - C = A, o seguinte é imediatamente obtido:
Exercícios Práticos para o Módulo de Trigonometria 2: Funções Trigonométricas & Identidades
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||