| |
Conteúdo do Módulo de Trigonometria 3: Problemas sobre Alturas e Distâncias
Trigonometria, nos tempos antigos, era usada com frequência na medida de alturas e distâncias de objetos que não poderiam ser medidos de outra forma. Por exemplo, trigonometria era usada para encontrar a distância entre estrelas e a Terra. Até hoje, independente de outros métodos mais precisos estarem disponíveis, trigonometria é constantemente usada para se fazer cálculos simples e rápidos em relação a alturas e distâncias de objetos distantes. Por isso o valor de várias funções trigonométricas é necessário. Um simples exemplo é dado abaixo para demonstrar como a trigonometria pode ajudar a encontrar a altura ou distância de um objeto.
Se a distância entre uma pessoa e uma torre é 100 m e o ângulo formado pelo topo da torre e o chão é30o, qual a altura da torre em metros?
Passos:
- Desenhe um simples diagrama para representar o problema.
Nomeie cuidadosamente e claramente marque os valores que são dados e os que precisam ser calculados.
Denote a dimensão desconhecida por digamos h se você estiver calculando a altura ou por x se você estiver calculando a distância.
- Identifique qual função trigonométrica representa a razão do lado sobre o qual informação é dada e o lado cujas dimensões se quer descobrir.
Monte uma equação trigonométrica.
- Substitua o valor da função trigonométrica e resolva a equação para a variável desconhecida.
Solução:
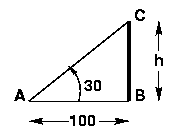
- AB = distância entre o homem e a torre = 100 m
- BC = altura da torre = h (a ser calculada)
- A função trigonométrica que usa AB e BC é tan A , onde A = 30o.
| Então tan 30o
= BC / AB = h / 100 |
Portanto a altura da torre é h = 100 tan 30o
= (100) 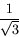 = 57.74 m.
= 57.74 m. |
|
A maioria dos problemas simples de trigonometria podem ser resolvidos pelo método ilustrado no exemplo acima.
Várias perguntas sobre Alturas e Distâncias em Trigonometria estão disponíveis juntamente com suas soluções nos exercícios práticos.
Exercícios Práticos para o Módulo de Trigonometria 3: Problemas sobre Alturas e Distâncias
| |
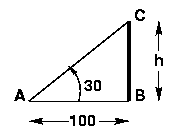
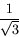 = 57.74 m.
= 57.74 m.